Reconstitution des voyages
Principes
A partir des données collectées, l'algorithme reconstitue les voyages en quatre étapes :
- reconstitution d'une partie des combinaisons entrée - sortie par la méthode des voyages consécutifs ;
- reconstitution de la course sur laquelle le voyage a été effectué, et de l'heure d'entrée ou sortie si manquante ;
- reconstitution des combinaisons entrée-sortie via le modèle stat par utilisateur
- reconstitution des combinaisons entrée - sortie restantes par la méthode statistique
L'une des difficultés de cette première étape est qu'une station peut être constituée de plusieurs arrêts, et qu'en fonction du réseau, on ne sait pas toujours, au moment où le voyageur valide, quelle ligne et quelle direction il emprunte.
Le but est de reconstituer des combinaisons d'entrées et de sorties enregistrées sur une ligne du réseau.
En fonction des caractéristiques du réseau, deux cas de figure peuvent se présenter. Pour un même titre de transport :
- on ne connaît que l'arrêt d'entrée ou de sortie de la ligne (cas 1) ;
- on connaît à la fois l'arrêt d'entrée et de sortie de la ligne (cas 2).
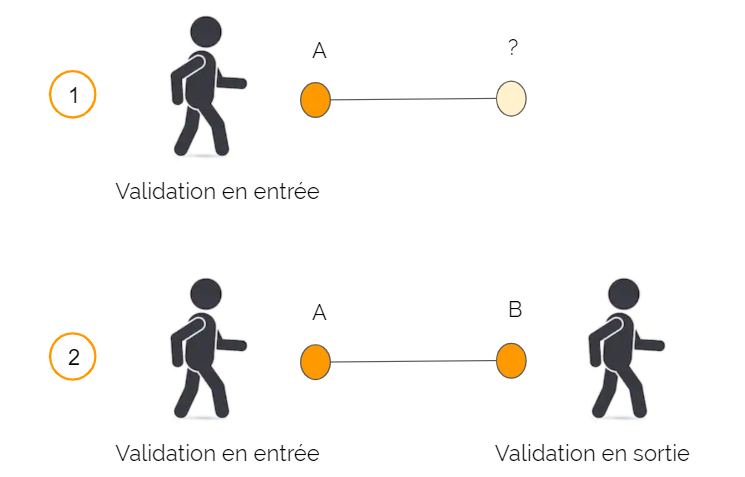
Le cas le plus fréquent est celui où on ne connaît que l'arrêt d'entrée (cas 1) : la plupart des réseaux imposent en effet de valider le titre de transport à l'entrée uniquement (quand on monte dans un bus par exemple).
L'enjeu de cette étape est donc d'inférer algorithmiquement l'information manquante (généralement la sortie) afin de reconstituer un maximum de combinaisons entrée - sortie, c'est à dire de voyages avec une origine et une destination. Pour cela, l'algorithme tente successivement trois approches :
- une approche à partir des entrées successives dans l'historique des validations (méthode des voyages consécutifs, étape 1) ;
- une approche centrée sur l'utilisateur, utilisant ses habitudes de déplacement (étape 3)
- une approche statistique exploitant tout l'historique des validations, et des comptages lorsque c'est possible (étape 4).
1. Méthode des voyages consécutifs
Pour toutes les combinaisons incomplètes d'entrée - sortie (entrée ou sortie manquante), l'algorithme examine les validations précédentes et suivantes du même numéro de suivi (identifiant unique du titre de transport), 24h après (respectivement 24h avant) la validation en entrée (respectivement la validation en sortie) analysée.
Par exemple :
Si je valide à la station A le matin du jour J, puis à la station B le soir du même jour J, il est vraisemblable que je sois allé(e) de A à B le matin. L'algorithme peut donc reconstituer une combinaison entrée - sortie A > B (cas 1).
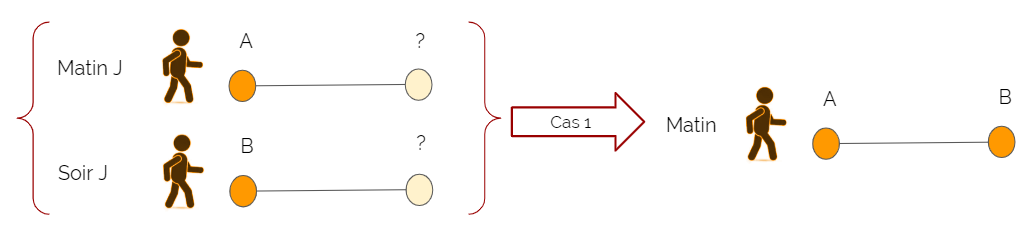
Voir quelques exemples supplémentaires en Annexe 1.
Cette méthode est particulièrement adaptée :
- sur les réseaux avec un taux d'abonnés élevés ou dont les titres unitaires peuvent être achetés sur des supports rechargeables, car elle s'applique aux validations pour lesquelles on dispose d'un numéro de suivi (identifiant unique du titre de transport) ;
- sur les réseaux où les mouvements pendulaires (domicile → travail ou domicile → lieu d'étude) sont prédominants ;
- sur les réseaux constitués de plusieurs lignes, où les usagers peuvent réaliser un déplacement avec correspondance(s) avec un même titre de transport.
Cette méthode ne peut pas être appliquée dans les cas suivants :
- titre de transport unitaire, avec une seule validation ;
- aucune autre validation 24h avant ou après ;
- pas de correspondance plausible entre les deux validations.
Dans ces cas, la méthode statistique (étape 3) est utilisée, après avoir associé une course à chaque trajet (étape 2).
Prise en compte de la direction des validations
L'information de direction, parfois disponible dans les données billettiques, peut améliorer la fiabilité des résultats. Si l'information est disponible, l'algorithme vérifie que la direction calculée par la méthode des voyages consécutifs est bien cohérente avec la direction inscrite dans les données.
Ainsi :
- si la direction est cohérente, aucune modification n'est apportée ;
- si la direction n'est pas cohérente, l'algorithme ne reconstitue pas la combinaison entrée - sortie avec la méthode des voyages consécutifs, et bascule sur la méthode statistique ;
- si on connaît à la fois l'arrêt d'entrée et l'arrêt de sortie, nous considérons que cette information est plus fiable que la direction inscrite dans les données. La direction n'est donc pas prise en compte ;
- dans la méthode statistique, la direction est prise en compte pour attribuer l'élément manquant (entrée ou sortie).
2. Correspondances avec les courses
Après la reconstitution des combinaisons entrée - sortie par la méthode des voyages consécutifs (étape 1), l'algorithme va rechercher la course correspondant à chaque combinaison reconstituée. On cherche ainsi à déterminer sur quelle course le passager s'est déplacé, afin de reconstituer la charge par course.
A noter que nous faisons l'hypothèse que les différents systèmes (billettiques et SAE) sont bien synchronisés temporellement.
La correspondance entre une validation et une course se fait en trois étapes :
- Identification des courses "probables" (+/- 30min d'écart avec l'heure de validation) ;
- Recherche d'une correspondance entre course et validations à partir du numéro de véhicule ;
- Si aucune correspondance n'a été trouvée (numéro de véhicule indisponible ou incohérent entre la validation et les courses), une correspondance est recherchée à partir de :
- l'heure de la validation ;
- l'heure de passage de la course à la même station ;
- la distinction entre les validations à bord et les validations à quai.
Les différentes étapes sont détaillées en Annexe 2.
Le modèle stat par utilisateur (étape 3) et la méthode statistique (étape 4) s'appuient sur les courses attribuées à chaque trajet.
3. Modèle stat par utilisateur
Avant de basculer sur une approche probabiliste plus générale pour les combinaisons entrée - sortie qui n'ont pas pu être traitées par la méthode des voyages consécutifs, un traitement spécifique est fait pour les données des voyageurs qui ont réalisé plusieurs trajets dans le mois.
L'objectif est de capturer le fait que certains voyageurs font souvent les mêmes trajets. Si on n'a pas pu trouver à l'étape 1 de combinaison entrée-sortie pour tous ces voyages, on peut les inférer en analysant l'historique du voyageur.
Pour chaque voyageur ayant réalisé plusieurs trajets dans le mois, et pour chaque entrée dans le réseau dont on n'a pas pu déterminer la sortie à l'étape 1 :
- on examine les voyages reconstitués à l'étape 1 sur la même ligne, direction, et station d'entrée ;
- on recherche le plus proche en termes d'heure de départ (via un système de scoring basé sur une gaussienne centrée sur l'heure de départ du voyage à compléter) ;
- on vérifie que le voyage est possible, c'est-à-dire qu'il y a eu une course à ce moment-là reliant la station d'entrée et la station de sortie, par le mécanisme présenté à l'étape 2.
Si aucun voyage complété à l'étape 1 ne correspond à ces critères, la validation sera traitée à l'étape suivante.
4. Méthode statistique
Dans les cas où ni la première méthode (étape 1), ni la deuxième (étape 3) ne permet de reconstituer une combinaison entrée - sortie à partir des voyages consécutifs d'une même personne (ou plus précisément, de son titre de transport), l'algorithme bascule sur la méthode statistique.
On applique d'abord une méthode globale par chaînage, puis dans certains cas on complète l'estimation par la méthode par course qui exploite des données de comptage lorsqu'elles sont disponibles.
4.1. Méthode statistique par chaînage, sans comptages
Cette méthode se base sur l'ensemble des combinaisons entrées - sorties connues ou reconstituées par la méthode des voyages consécutifs, sur l'ensemble des types de titres de transport, sur les 8 semaines précédentes, et en distinguant quatre types de jours : les jours de semaine du lundi au jeudi, le vendredi, le samedi et le dimanche.
A partir de cet ensemble de combinaisons, l'algorithme calcule la fréquence globale de chaque voyage et en infère :
- pour chaque arrêt d'entrée, une première probabilité de sortie à chaque arrêt de la ligne ;
- pour chaque arrêt de sortie, une première probabilité d'entrée à chaque arrêt de la ligne.
Par exemple : considérons une ligne de 3 stations dans la direction A → C. Avec le nombre de trajets reconstitués grâce à la méthode des voyages consécutifs, on peut calculer ces premières probabilités.
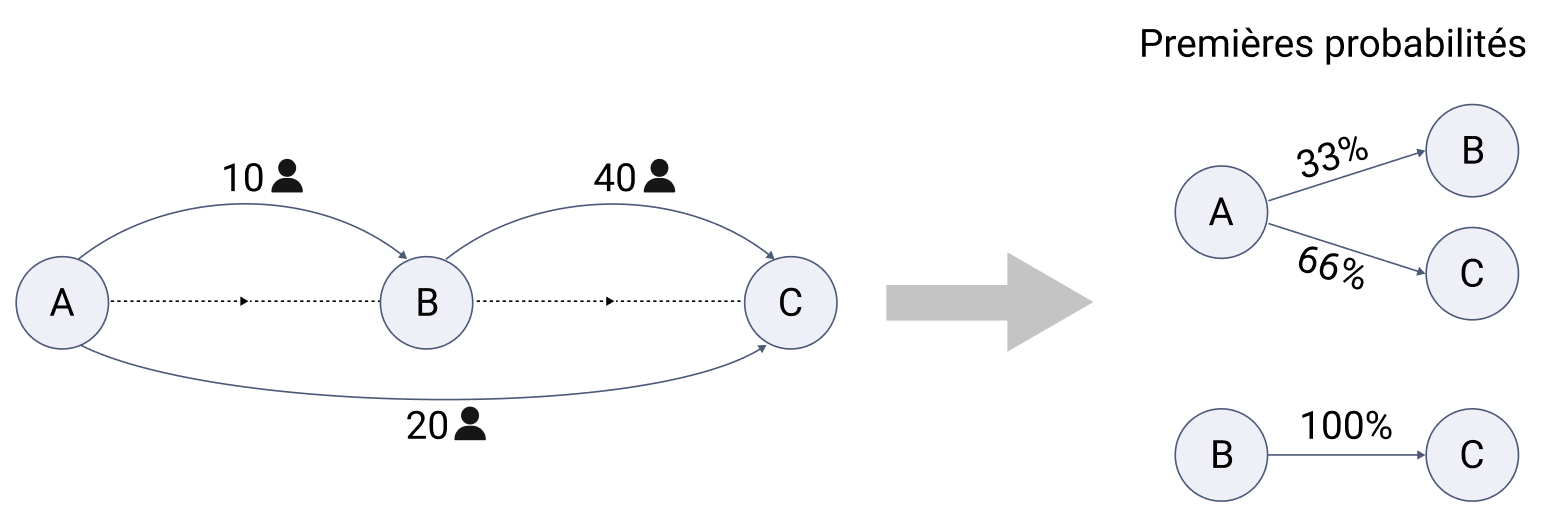
Ces premières probabilités sont ensuite rectifiées à partir des fréquences globales de descentes de voyageurs par station. Par exemple, si 80% des sorties sur un chaînage se font au terminus, il faut que ce soit le cas des voyages pour chaque arrêt d'entrée.
Ces fréquences sont calculées à partir de l'ensemble des validations du réseau, en faisant l'hypothèse que le nombre de descentes à une station sur une ligne dans une direction est égal (sur une période de temps large, actuellement 8 semaines) au nombre de montées à cette même station sur cette ligne mais dans l'autre direction.
Par exemple : considérons une ligne de 3 stations A, B, C. Avec le nombre de validations en entrée à chaque station dans les deux directions sur 8 semaines, on peut calculer les fréquences globales de descentes.
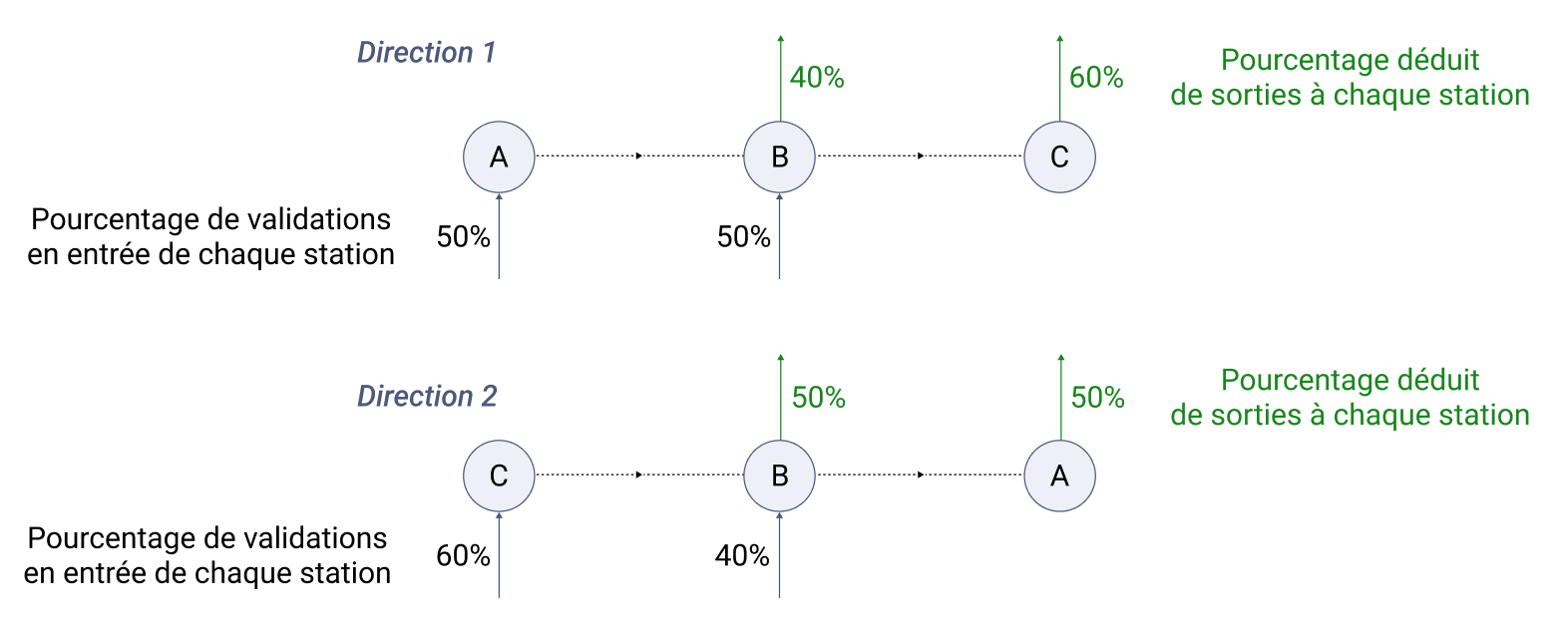
Ainsi on prend en compte l'éventuelle différence de comportement entre les usagers ponctuels et les voyageurs réguliers du réseau.
Les premières probabilités et les fréquences globales de descentes sont ensuite combinées pour obtenir les probabilités finales.
4.2. Optionnel : méthode statistique par course, avec comptages
Dans certains cas et à la condition que des données de comptage soient disponibles, un algorithme supplémentaire vient encore améliorer la précision de ces probabilités.
Cet algorithme exploite les données des cellules de comptages. Cela permet :
- d'avoir une connaissance de cette fréquentation plus globale que si on utilisait uniquement les données billettiques ;
- de moins s'appuyer sur les déplacements pendulaires, et plus généralement sur les déplacements effectués par les voyageurs réguliers.
Il comprend plusieurs étapes :
- Calcul des taux de fraude globaux pour chaque station de chaque chaînage ;
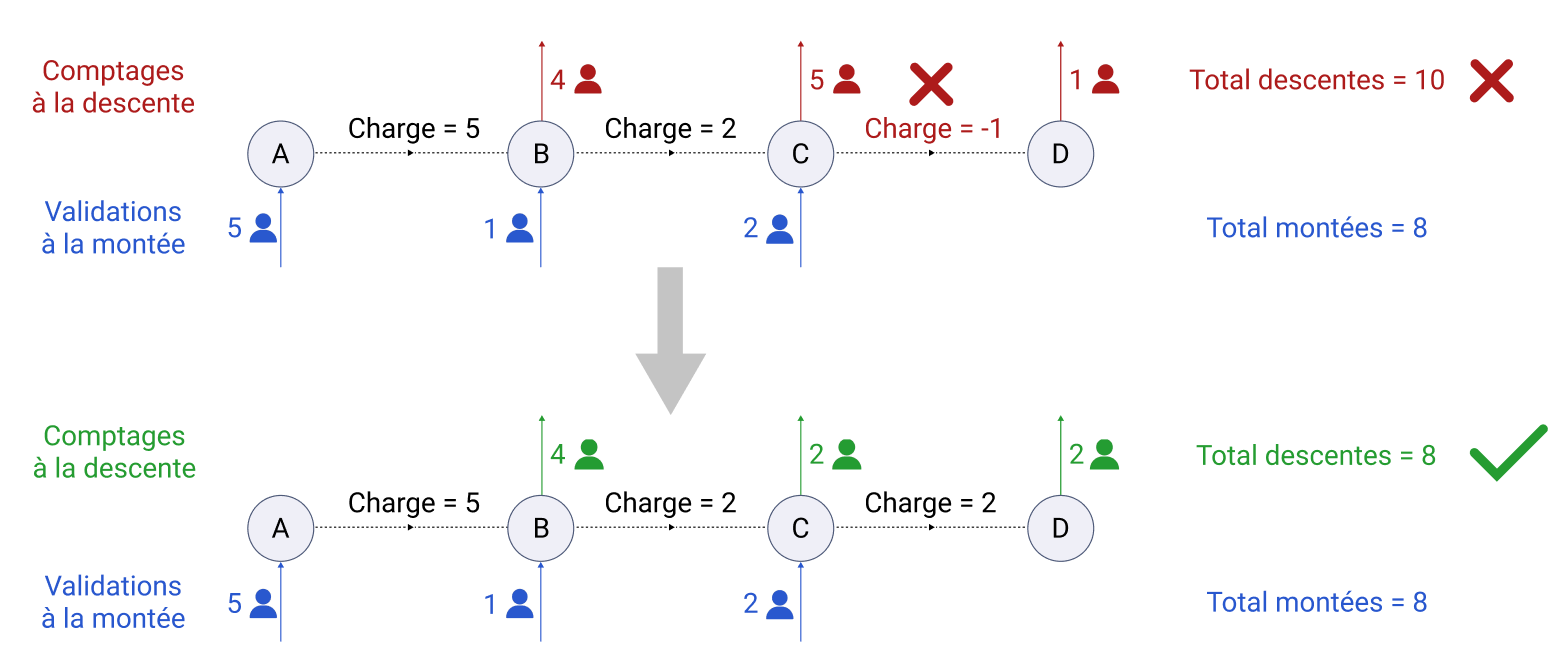
- Débruitage des données de comptage de chaque course équipée en soustrayant la fraude et en faisant en sorte de respecter les contraintes d'une course valide (voir exemple ci-dessous) :
- Estimation des probabilités de descentes spécifiques à la course en combinant les probabilités obtenues à l'étape précédente 3.1 (modèle statistique sans comptages, qui donne des probabilités globales par chaînage) avec les données de comptage débruitées.
Par exemple : sur une course de 4 stations, on ajuste les comptages de sortie pour respecter les contraintes vis à vis du nombre de validations en entrée.
Ce modèle s'applique donc uniquement aux courses réalisées par des véhicules équipés de cellules de comptages.
4.3. Application des probabilités estimées aux combinaisons incomplètes
Que la méthode par course soit ou non utilisée pour renforcer l'estimation des probabilités (3.1 seul, ou 3.1 suivi de 3.2), chaque combinaison entrée - sortie incomplète se voit finalement attribuer l'élément manquant en fonction de ces probabilités (de manière aléatoire mais reproductible).
L'étape de correspondance avec les courses (étape 2) est de nouveau appliquée, afin de vérifier la conformité des combinaisons complétées avec la course initialement attribuée.
5. Résultats
A la fin de cette étape, nous avons donc une liste de voyages avec les informations suivantes:
- station d'entrée et de sortie ;
- heure d'entrée et de sortie ;
- course correspondante.
Si aucune course ne correspond aux différents critères, la combinaison entrée - sortie est éliminée et n'est pas prise en compte dans le calcul de la charge.
Les voyages ainsi obtenus constituent la fin de la première étape de reconstitution des flux Origines - Destinations. Il faut à présent prendre en compte les correspondances pour reconstituer des déplacements.
Autres pages
Reconstitution des flux Origine - Destination et de la charge
